|
|
|
|
|
Next: 4.2 Angular Momentum |
|
This section provides an in-depth discussion of a basic quantum system. The case to be analyzed is a particle that is constrained by some kind of forces to remain at approximately the same position. This can describe systems such as an atom in a solid or in a molecule. If the forces pushing the particle back to its nominal position are proportional to the distance that the particle moves away from it, you have what is called an harmonic oscillator. Even if the forces vary nonlinearly with position, they can often still be approximated to vary linearly as long as the distances from the nominal position remain small.
The particle’s displacement from the nominal position will be
indicated by ![]() .
.
The stiffness of the springs is characterized by the so called
spring constant
![]() ,
,
For a quantum picture of a harmonic oscillator, imagine a light atom like a carbon atom surrounded by much heavier atoms. When the carbon atom tries to move away from its nominal position, the heavy atoms push it back. The harmonic oscillator is also the basic relativistic model for the quantum electromagnetic field.
According to classical Newtonian physics, the particle vibrates back
and forth around its nominal position with a frequency
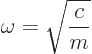 |
(4.1) |
Key Points
- The system to be described is that of a particle held in place by forces that increase proportional to the distance that the particle moves away from its equilibrium position.
- The relation between distance and force is assumed to be the same in all three coordinate directions.
- Number
is a measure of the strength of the forces and is the frequency of vibration according to classical physics.
In order to find the energy levels that the oscillating particle can have, you must first write down the total energy Hamiltonian.
As far as the potential energy is concerned, the spring in the
![]() -
-![]() ,
,![]()
![]()
To this total potential energy, you need to add the kinetic energy
operator ![]()
Key Points
- The Hamiltonian (4.2) has been found.
This section finds the energy eigenfunctions and eigenvalues of the
harmonic oscillator using the Hamiltonian as found in the previous
subsection. Every energy eigenfunction ![]()
![]()
time-independent Schrödinger equation
):
![\begin{displaymath}
\left[- \frac{\hbar^2}{2m}
\left(
\frac{\partial^2}{\part...
...e\frac{1}{2}}c \left(x^2+y^2+z^2\right)
\right] \psi = E \psi
\end{displaymath}](img512.gif) |
(4.3) |
Like for the particle in the pipe of the previous section, it will be
assumed that each eigenfunction is a product of one-dimensional
eigenfunctions, one in each direction:
| (4.4) |
Substituting the assumption in the eigenvalue problem above, and
dividing everything by ![]()
![]() ,
,![]() ,
,![]() :
:
![\begin{displaymath}
\begin{array}{l}
\displaystyle \rule[-1ex]{0pt}{2ex}
E = ...
..._z''(z)}{\psi_z(z)} + {\textstyle\frac{1}{2}}c z^2
\end{array}\end{displaymath}](img518.gif) |
(4.5) |
By the definition above, the quantity ![]()
![]() ;
;![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]() .
.![]()
![]()
If now in the definition of ![]()
![]() ,
,
![\begin{displaymath}
\left[
- \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2}
+ {\textstyle\frac{1}{2}} c x^2
\right]
\psi_x = E_x \psi_x
\end{displaymath}](img521.gif) |
(4.6) |
Solving the one-dimensional problem for ![]()
![]()
![]() :
:
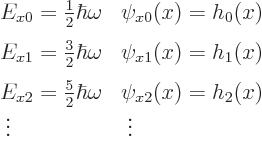 |
(4.7) |
Also, the eigenfunctions are not sines like for the particle in the pipe; instead, as table 4.1 shows, they take the form of some polynomial times an exponential. But you will probably really not care much about what kind of functions they are anyway unless you end up writing a textbook on quantum mechanics and have to plot them. In that case, you can find a general expression, (D.4), in derivation {D.12}.
But the eigenvalues are what you want to remember from this solution.
According to the orthodox interpretation, these are the measurable
values of the total energy in the ![]() -
-![]() -
-![]() -
-
| (4.8) |
The eigenvalue problem has now been solved, because the equations for
![]()
![]()
| (4.9) |
| (4.10) |
The total energy ![]()
![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
quantum numbers
The corresponding eigenfunction of the complete system is:
Note that the ![]()
Key Points
- The eigenvalues and eigenfunctions have been found, skipping a lot of tedious math that you can check when the weather is bad during spring break.
- Generic expressions for the eigenvalues are above in (4.11) and for the eigenfunctions in (4.12).
Write out the ground state energy.
Write out the ground state wave function fully.
Write out the energy ![]() .
.
Write out the eigenstate ![]()
As the previous subsection showed, for every set of three nonnegative
whole numbers ![]() ,
,![]() ,
,![]() ,
,![]()
This section will examine the energy eigenvalues. These are of great physical importance, because according to the orthodox interpretation, they are the only measurable values of the total energy, the only energy levels that the oscillator can ever be found at.
The energy levels can be plotted in the form of a so-called “energy spectrum”, as in figure 4.2. The energy
values are listed along the vertical axis, and the sets of quantum
numbers ![]()
The first point of interest illustrated by the energy spectrum is that
the energy of the oscillating particle cannot take on any arbitrary
value, but only certain discrete values. Of course, that is just like
for the particle in the pipe of the previous section, but for the
harmonic oscillator, the energy levels are evenly spaced. In
particular the energy value is always an odd multiple of
![]() .
.![]()
![]()
![]() /
/
Also note that the energy levels have no largest value; however high the energy of the particle in a true harmonic oscillator may be, it will never escape. The further it tries to go, the larger the forces that pull it back. It can’t win.
Another striking feature of the energy spectrum is that the lowest
possible energy is again nonzero. The lowest energy occurs for
![]()
![]()
![]()
![]()
![]()
![]()
| (4.13) |
The reason that the energy cannot be zero can be understood from the uncertainty principle. To get the potential energy to be zero, the particle would have to be at its nominal position for certain. But the uncertainty principle does not allow a precise position. Also, to get the kinetic energy to be zero, the linear momentum would have to be zero for certain, and the uncertainty principle does not allow that either.
The actual ground state is a compromise between uncertainties in momentum and position that make the total energy as small as Heisenberg's relationship allows. There is enough uncertainty in momentum to keep the particle near the nominal position, minimizing potential energy, but there is still enough uncertainty in position to keep the momentum low, minimizing kinetic energy. In fact, the compromise results in potential and kinetic energies that are exactly equal, {D.13}.
For energy levels above the ground state, figure 4.2
shows that there is a rapidly increasing number of different sets of
quantum numbers ![]() ,
,![]() ,
,![]()
Key Points
- Energy values can be graphically represented as an energy spectrum.
- The energy values of the harmonic oscillator are equally spaced, with a constant energy difference of
between successive levels.
- The ground state of lowest energy has nonzero kinetic and potential energy.
- For any energy level above the ground state, there is more than one eigenstate that produces that energy.
Verify that the sets of quantum numbers shown in the spectrum figure 4.2 do indeed produce the indicated energy levels.
Verify that there are no sets of quantum numbers missing in the spectrum figure 4.2; the listed ones are the only ones that produce those energy levels.
This section takes a look at the energy eigenfunctions of the harmonic oscillator to see what can be said about the position of the particle at various energy levels.
At absolute zero temperature, the particle will be in the ground state of lowest energy. The eigenfunction describing this
state has the lowest possible numbering ![]()
![]()
![]()
![]()
![]()
![]()
| (4.14) |
| (4.15) |
As noted earlier in section 3.1, it is useful to plot
the square magnitude of ![]()
The region in which the particle is likely to be found extends,
roughly speaking, about a distance ![]()
![]()
![]()
![]() .
.![]()
![]()
But obviously, the bad news is that the ground state probability density of figure 4.3 does not at all resemble the classical Newtonian picture of a localized particle oscillating back and forwards. In fact, the probability density does not even depend on time: the chances of finding the particle in any given location are the same for all times. The probability density is also spherically symmetric; it only depends on the distance from the nominal position, and is the same at all angular orientations. To get something that can start to resemble a Newtonian spring-mass oscillator, one requirement is that the energy is well above the ground level.
Turning now to the second lowest energy level, this energy level is
achieved by three different energy eigenfunctions, ![]() ,
,![]() ,
,![]() .
.blobs
; figure 4.4 shows ![]()
![]()
![]() -
-![]() ,
,
Obviously, these states too do not resemble a Newtonian oscillator at all. The probability distributions once again stay the same at all times. (This is a consequence of energy conservation, as discussed later in chapter 7.1.) Also, while in each case there are two blobs occupied by a single particle, the particle will never be be caught on the symmetry plane in between the blobs, which naively could be taken as a sign of the particle moving from one blob to the other.
The eigenfunctions for still higher energy levels show similar lack of
resemblance to the classical motion. As an arbitrary example, figure
4.5 shows eigenfunction ![]()
![]() -
-
The basic reason that quantum mechanics is so slow is simple. To
analyze, say the ![]()
![]()
Key Points
- The ground state wave function is spherically symmetric: it looks the same seen from any angle.
- In energy eigenstates the particle position is uncertain.
Write out the ground state wave function and show that it is indeed spherically symmetric.
Show that the ground state wave function is maximal at the origin and, like all the other energy eigenfunctions, becomes zero at large distances from the origin.
Write down the explicit expression for the eigenstate ![]()
![]() -
-![]() -
-![]() -
-
As the energy spectrum figure 4.2 illustrated, the only
energy level for which there is only a single energy eigenfunction is
the ground state. All higher energy levels are what is called
degenerate
; there is more than one eigenfunction that
produces that energy. (In other words, more than one set of three
quantum numbers ![]() ,
,![]() ,
,![]() .
.
It turns out that degeneracy always results in nonuniqueness of the eigenfunctions. That is important for a variety of reasons. For example, in the quantum mechanics of molecules, chemical bonds often select among nonunique theoretical solutions those that best fit the given conditions. Also, to find specific mathematical or numerical solutions for the eigenfunctions of a quantum system, the nonuniquenesses will somehow have to be resolved.
Nonuniqueness also poses problems for advanced analysis. For example, suppose you try to analyze the effect of various small perturbations that a harmonic oscillator might experience in real life. Analyzing the effect of small perturbations is typically a relatively easy mathematical problem: the perturbation will slightly change an eigenfunction, but it can still be approximated by the unperturbed one. So, if you know the unperturbed eigenfunction you are in business; unfortunately, if the unperturbed eigenfunction is not unique, you may not know which is the right one to use in the analysis.
The nonuniqueness arises from the fact that:
Linear combinations of eigenfunctions at the same energy level produce alternative eigenfunctions that still have that same energy level.
For example, the eigenfunctions ![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
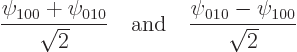
Which raises the question, how come the analysis ended up with the
ones that it did in the first place? The answer is in the method of
separation of variables that was used in subsection 4.1.2.
It produced eigenfunctions of the form
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
For example, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.
The alternative eigenfunctions are still eigenfunctions of ![]() ,
,
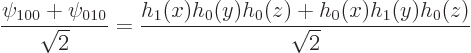
So, the obtained eigenfunctions were really made determinate by
ensuring that they are simultaneously eigenfunctions of ![]() ,
,![]() ,
,![]() ,
,![]() .
.
Key Points
- Degeneracy occurs when different eigenfunctions produce the same energy.
- It causes nonuniqueness: alternative eigenfunctions will exist.
- That can make various analysis a lot more complex.
Just to check that this book is not lying, (you cannot be too careful), write down the analytical expression for ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() -
-![]()
It should not be thought that the harmonic oscillator only exists in energy eigenstates. The opposite is more like it. Anything that somewhat localizes the particle will produce an uncertainty in energy. This section explores the procedures to deal with states that are not energy eigenstates.
First, even if the wave function is not an energy eigenfunction, it
can still always be written as a combination of the eigenfunctions:
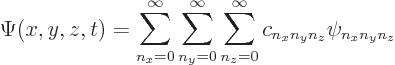 |
(4.16) |
The coefficients ![]()
![]() .
.![]()
If the wave function ![]()
![]()
| (4.17) |
The reason this works is orthonormality of the eigenfunctions. As an
example, consider the case of coefficient ![]() :
:
Chapter 7.1 will discuss another reason why the coefficients are important: they determine the time evolution of the wave function. It may be recalled that the Hamiltonian, and hence the eigenfunctions derived from it, did not involve time. However, the coefficients do.
Even if the wave function is initially in a state involving many
eigenfunctions, such as the one in figure 4.6, the
orthodox interpretation says that energy measurement
will collapse it into a single eigenfunction. For example, assume
that the energies in all three coordinate directions are measured and
that they return the values:
After the example measurement, the predictions become much more
specific, because the wave function is now collapsed into the measured
one:
If another measurement of the energies is now done, the only values
that can come out are ![]() ,
,![]() ,
,![]() ,
,![]()
![]()
Key Points
- The basic ideas of quantum mechanics were illustrated using an example.
- The energy eigenfunctions are not the only game in town. Their seemingly lowly coefficients are important too.
- When the wave function is known, the coefficient of any eigenfunction can be found by taking an inner product of the wave function with that eigenfunction.