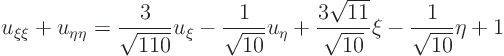18.8 Two-Dimensional Coordinate Transforms

More powerful simplifications by changing coordinates are possible in 2D.

Assume that in terms of coordinates $x$ and $y$, we have a partial differential equation:

$$a u_{xx} + 2 b u_{xy} + c u_{yy} = d$$

Then, if we transform to new coordinates, call them $\xi$ and $\eta$, we will get a new partial differential equation of the form: $\xi,\eta$

$$a' u_{\xi\xi} + 2 b' u_{\xi\eta} + c' u_{\eta\eta} = d'$$

The idea is again to choose the new coordinates $\xi$ and $\eta$ so that the new partial differential equation is as simple as possible.

For example, for a hyperbolic equation, you may like coordinates $\xi$ and $\eta$ such that $a'$ and $c'$ are zero. To find out for what coordinates $\xi$ and $\eta$ that is the case, expressions for the new coefficients $a'$, $b'$, $c'$ and $d'$ in terms of the new coordinates are needed. These can be found by writing out the general transformation formulae from section 18.7.2 for the special case of two dimensions. You get, {D.5}:

$$\fbox{$\displaystyle \begin{array}{l} a' = a \left(\... ... b \eta_{xy} + c \eta_{yy}\right) u_\eta \end{array} $} %$$ (18.22)

18.8.1 Characteristic Coordinates

Characteristic coordinates are coordinates so that the the $u_{\xi\xi}$ and $u_{\eta\eta}$ derivatives are eliminated. That leaves only the $u_{\xi\eta}$ derivative, greatly simplifying the partial differential equation. It reduces to the two-di­men­sion­al canonical form:

$$\fbox{$\displaystyle 2 b' u_{\xi\eta} = d' $}$$ (18.23)

The first thing is to find out how this may be achieved. In terms of the coefficients of the transformed equation as discussed above, $a'$ and $c'$ must vanish. The condition $a'$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 requires, according to the given formulae:

$$a \left(\xi_x\right)^2 + 2b \left(\xi_x\right)\left(\xi_y\right) + c \left(\xi_y\right)^2 = 0$$

That can be considered to be a partial differential equation for $\xi$. A nonlinear first order equation, to be sure. Similarly for $c'$ to vanish,

$$a \left(\eta_x\right)^2 + 2b \left(\eta_x\right)\left(\eta_y\right) + c \left(\eta_y\right)^2 = 0$$

Note that $\xi$ and $\eta$ must satisfy the exact same equation, but they must be different solutions. Otherwise they are not valid independent coordinates.

To solve the equation for $\xi$ ($\eta$ goes the same way), divide by $\left(\xi_y\right)^2$:

$$a \left(-\frac{\xi_x}{\xi_y}\right)^2 - 2b \left(-\frac{\xi_x}{\xi_y}\right) + c = 0$$

and note that, from your calculus or thermo,

$$-\frac{\xi_x}{\xi_y} = \left(\frac{{\rm d}y}{{\rm d}x}\right)_{\hbox{$\xi$ is constant}}$$

So the lines of constant $\xi$ should satisfy the ordinary differential equation

$$\fbox{$\displaystyle \frac{{\rm d}y}{{\rm d}x} = \frac{b \pm \sqrt{b^2-ac}}{a} $} %$$

We can achieve this by taking $\xi$ to be the integration constant in the solution of this ordinary differential equation! Integration constants are, like the word says, constant for solutions.

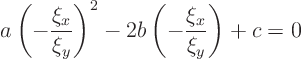
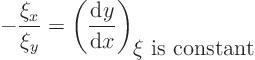
By taking the other sign for the square root, you can get a second independent coordinate $\eta$.

Bottom line, to get characteristic coordinates, solve the plus and minus sign ordinary differential equations above, and equate the integration constants to $\xi$ and $\eta$.

A couple of notes:

1. Since integration constants are not unique, the characteristic coordinates are not. But the lines of constant $\xi$ and $\eta$ are unique, and are called characteristic lines or characteristics.
2. Elliptic equations do not have characteristics, because the square root in the ordinary differential equation would be imaginary. The coordinates $\xi$ and $\eta$ must be real; you do not want to deal with partial differential equations in complex coordinates.
3. Parabolic equations have only one family of characteristic lines. That is because the square root is zero, so taking the other root does not make a difference.

Example

Question: Use characteristic coordinates to reduce the wave equation in multi-di­men­sion­al canonical form

$$u_{tt} - a^2 u_{xx} = 0$$

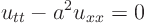
to its equivalent two-di­men­sion­al canonical form. Then solve it.

Solution:

First find the characteristics by solving the ordinary differential equation given above:

$$\frac{{\rm d}x}{{\rm d}t} = \frac{b \pm \sqrt{b^2-ac}}{a} = \pm a$$

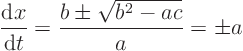
Note that the final $a$ is the wave propagation speed, not the coefficient $a$ in the generic second order equation.

The solution is simple:

$$x = at + \xi \qquad x = -at + \eta$$

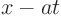
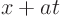
where $\xi$ and $\eta$ are the integration constants (as well as the characteristic coordinates). So the lines $x-at$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\mbox{constant}$ are one set of characteristic lines, and the lines $x+at$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\mbox{constant}$ are the other set.

Now find the coefficient $d'$. The coefficient $d$ was zero, and the second order derivatives of $\xi$ and $\eta$ in the formula for $d'$ are also zero, so $d'$ is zero too. So the wave equation in characteristic coordinates is

$$\fbox{$\displaystyle u_{\xi\eta} = 0 $}$$ (18.24)

Note that $b'$ could be divided out, so there is no need to figure out what it is.

The wave equation can now easily be solved. Integration with respect to $\eta$ gives

$$u_\xi = f(\xi)$$

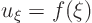
where the integration constant $f$ can be any arbitrary function of $\xi$. Integrating with respect to $\xi$ gives the final solution:

$$u = f_1(\xi)+f_2(\eta)$$

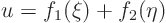
Here $f_1$ is an antiderivative of $f$, so it is arbitrary just like $f$. The additional integration constant $f_2$ is an arbitrary function of $\eta$.

However, you would surely want the solution in terms of the physical coordinates $x$ and $t$, rather than the mathematical characteristic coordinates. So substitute for $\xi$ and $\eta$ using the obtained equations for the characteristics. That gives the final solution:

$$\fbox{$\displaystyle u = f_1(x-at)+f_2(x+at) $}$$ (18.25)

That is the general solution of the wave equation. In order to solve a particular problem, you will still need to figure out what $f_1$ and $f_2$ are using whatever the initial and boundary conditions are. One special case, in which the $x$-range is doubly infinite, will be solved in detail later.

Example

Question: Find and sketch the characteristics of the equation

$$u_{xx} + y u_{yy} = 0$$

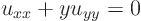
Solution:

Figure out the coefficients in the the characteristic equation by looking at the partial differential equation:

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b\pm\sqrt{b^2 - ac}}{a} = \pm \sqrt{-y}$$

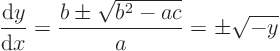
Note that there are only characteristics for negative $y$. For positive $y$ the equation is elliptic. And for zero $y$ there will only be one direction for the characteristics, horizontal.

Use separation of variables to solve. In other words, take the $y$ factors to one side and the $x$-factors to the other side:

$$\frac{{\rm d}- y}{\sqrt{-y}} = \pm {\rm d}x \quad\quad\Rightarrow\quad\quad 2 \sqrt{-y} = \pm (x - C)$$

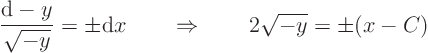
Squaring both sides to get rid of the square root gives

$$y = -{\textstyle\frac14}(x - C)^2$$

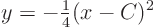
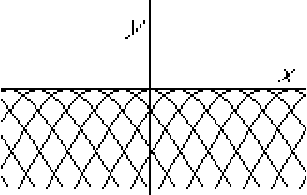
These are parabolae.

$$\hbox{\epsffile{chexamp1.eps}}$$

Example

Question: Reduce the equation

$$e^y u_{xx} + 2 e^x u_{xy} - e^{2x-y} u_{yy} = 0$$

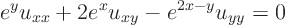
to two-di­men­sion­al canonical form.

Solution:

Two-di­men­sion­al canonical form means characteristic form. Find the ordinary differential equation for the characteristics:

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b\pm\sqrt{b^2 - ac}}{a} = (1\pm\sqrt{2}) e^{x-y}$$

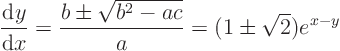
Solve it using separation of variables:

$$e^y {\rm d}y = (1 \pm \sqrt2) e^x {\rm d}x \quad\quad\Rightarrow\quad\quad e^y = (1 \pm \sqrt2) e^x + C$$

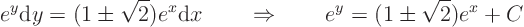
The integration constants are the new coordinates:

$$\xi = (1 + \sqrt2) e^x - e^y \qquad \eta = (1 - \sqrt2) e^x - e^y$$

Work out the partial differential equation in these coordinates using the formulae given at the start of this section:

$$b ' = a \left(\xi_x\right)\left(\eta_x\right) + b \lef... ...) + c \left(\xi_y\right)\left(\eta_y\right) = - 4 e^{2x+y}$$

$$d' = d - \left(a \xi_{xx} + 2 b \xi_{xy} + c \xi_{yy}\ri... ...left(a \eta_{xx} + 2 b \eta_{xy} + c \eta_{yy}\right) u_\eta$$

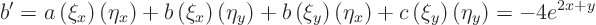
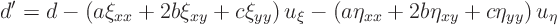
so

$$d' = - \left[(1+\sqrt2)e^{x+y}+ e^{2x}\right] u_\xi - \left[(1-\sqrt2)e^{x+y}+ e^{2x}\right] u_\eta$$

The partial differential equation becomes

$$8 e^{x+y} u_{\xi\eta} = \left[(1+\sqrt2)e^y+ e^x\right] u_\xi \left[(1-\sqrt2)e^y+ e^x\right] u_\eta$$

Get rid of $x$ and $y$ completely using the equations for the characteristics:

$$e^x = \frac{1}{2\sqrt2} (\xi-\eta) \quad e^y = - \frac{1-\sqrt2}{2\sqrt2} \xi- \frac{1+\sqrt2}{2\sqrt2}\eta$$

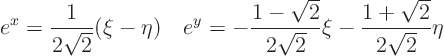
The resulting partial differential equation is

$$(\xi -\eta)[(1-\sqrt2)\xi + (1+\sqrt2)\eta]u_{\xi\eta} = (1+\sqrt2)\eta u_\xi + (1-\sqrt2)\xi u_\eta$$

It does not look easily solvable.

Example

Question: Find the characteristic coordinates of the equation

$$\sin^2 (x) u_{xx} + 2 \cos(x) u_{xy} - u_{yy} = 0$$

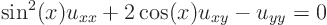
Solution:

Find the ordinary differential equation for the characteristics:

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b\pm\sqrt{b^2 - ac}}{a} = \frac{\cos(x) \pm 1}{\sin^2(x)}$$

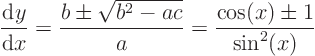
Solve it:

$$y = - \frac1{\sin(x)} \pm \hbox{cotg}(x) + C$$

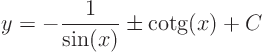
The characteristic coordinates are the integration constants:

$$\xi = y + \frac1{\sin(x)} + \hbox{cotg}(x) \quad \eta = y + \frac1{\sin(x)} - \hbox{cotg}(x)$$

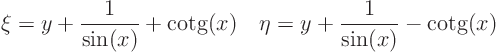
It does not look like the partial differential is going to be very simple.

18.8.2 Parabolic equations in two dimensions

In the parabolic case there is only one equation for the characteristics because the discriminant $b^2-ac$ is zero:

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b}{a}$$

So you can only find one characteristic coordinates, call it $\eta$.

You will need to take the other coordinate something else, say $\xi$ $\vphantom0\raisebox{1.5pt}{$=$}$ $x$. You want to take something simple, but it should be independent of the other coordinate.

The partial differential equations then simplifies to the two-di­men­sion­al canonical form

$$\fbox{$\displaystyle a' u_{\xi\xi} = d' $}$$ (18.26)

You may be surprised by that. In choosing $\eta$, all we did was make the coefficient $c'$ zero. We did not explicitly make $b'$ zero. But $b'$ is zero automatically. The reason is that the physical properties of partial differential equations do not change just because you use different coordinates. A parabolic equation should stay parabolic; there are fundamental differences between the physical behaviors of parabolic, elliptic, and hyperbolic equations. And the equation above would not be parabolic if $b'$ was nonzero.

Example

Question: Reduce the equation

$$x u_{xx} + 2 \sqrt{xy} u_{xy} + y u_{yy} - u_y = 0$$

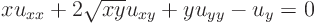
to two-di­men­sion­al canonical form.

Solution:

Write the equation for the characteristics

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b\pm\sqrt{b^2 - ac}}{a} = \sqrt{\frac yx}$$

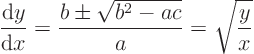
The square root is zero, so the equation is parabolic.

Solve the equation and call the integration constant $\eta$:

$$\frac{{\rm d}y}{\sqrt y} = \frac{{\rm d}x}{\sqrt x} \quad\quad\Rightarrow\quad\quad \sqrt y = \sqrt x + \eta$$

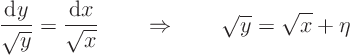
So take the new coordinates as

$$\xi = x \qquad \eta = \sqrt y - \sqrt x$$

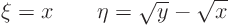
The final partial differential equation then becomes

$$- 4 \xi u_{\xi\xi} = \left[\frac{1}{\sqrt{\xi}} + \frac{3}{\eta+\sqrt{\xi}}\right] u_{\eta}$$

18.8.3 Elliptic equations in two dimensions

Characteristic lines are solutions to the ordinary differential equation

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b\pm\sqrt{b^2 - ac}}{a}$$

Elliptic equations have no real characteristics, because the square root is imaginary. However, elliptic equations can still be simplified, assuming that the above ordinary differential equation can be solved analytically.

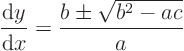
Take either sign of the square root. Solve the equation and call the integration constant, say, $\tilde\xi$. Then write this integration constant in the form

$$\fbox{$\displaystyle \tilde\xi = \xi + {\rm i}\eta $}$$ (18.27)

where $\xi$ and $\eta$ are real and ${\rm i}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\sqrt{-1}$. In other words, take $\xi$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\Re(\tilde\xi)$ and $\eta$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\Im(\tilde\xi)$.

Using $\xi$ and $\eta$ as the new coordinates, it turns out that the partial differential equation takes the two-di­men­sion­al canonical form:

$$\fbox{$\displaystyle a' u_{\xi\xi} + a' u_{\eta\eta} = d' $}$$ (18.28)

You may note that this is quite similar to what you can get from rotating the coordinate system, as in the previous section. However, the above procedure works even if the coefficients $a$, $b$, and $c$ of the original partial differential equation are not constants.

There are significant limitations on this procedure, however, {D.6}

Example

Question: Reduce the equation

$$u_{xx} + (1+y)^2 u_{yy} = 0$$

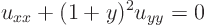
to two-di­men­sion­al canonical form.

Solution:

Write the equation for the characteristics

$$\frac{{\rm d}y}{{\rm d}x} = \frac{b\pm\sqrt{b^2 - ac}}{a} = \pm {\rm i}(1+y)$$

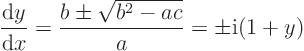
This is complex, so the equation is elliptic.

Solve using separation of variables

$$\frac{{\rm d}y}{1+y} = {\rm i}{ \rm d}x \quad\quad\Rightarrow\quad\quad \ln\vert 1+y\vert - {\rm i}x = \tilde\xi$$

The new coordinates can therefore be chosen as

$$\xi = \ln\vert 1+y\vert \qquad \eta = - x$$

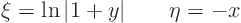
In terms of these coordinates, the equation becomes

$$a' u_{\xi\xi} + a' u_{\eta\eta} = d'$$

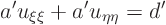
The new partial differential equation becomes

$$u_{\xi\xi} + u_{\eta\eta} = - u_\xi$$

18.8.3 Review Questions

1.

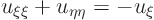
Convert the equation

$$10 u_{xx} + 6 u_{xy} + 2 u_{yy} = u_x + x + 1$$

to two-di­men­sion­al canonical form.

Using rotation and stretching of the coordinates you would get

$$u_{\xi\xi} + u_{\eta\eta} = \frac{3}{\sqrt{110}} u_{\xi} - \... ...frac{3\sqrt{11}}{\sqrt{10}} \xi - \frac{1}{\sqrt{10}} \eta + 1$$

Do you get the same equation? Should you? Comment.

Solution 2dcanel-a