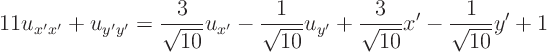|
|
|
|
|
Next: 18.8 Two-Dimensional Coordinate Transforms |
|
Changes of coordinates are a primary way to understand, simplify, and sometimes even solve, partial differential equations.
It is possible to simplify many partial differential equation problems by using coordinate systems that are special to the problem:
Assume the purpose is to address a problem in an ![]() -dimensional
space. The coordinates in this space form a vector
-dimensional
space. The coordinates in this space form a vector
The idea is now to switch to some new set of independent coordinates
The change of coordinates is characterized by Jacobian matrices
The complete Jacobian matrices describes how a small change in
![]() relates to the corresponding change in
relates to the corresponding change in ![]() , and vice
versa:
, and vice
versa:
In index notation, the components of the Jacobian matrices are
The purpose is now to simplify second order quasi-linear partial
differential equations using coordinate transforms. As noted in the
previous section, second order quasi-linear equations are of the form
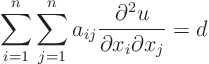
Of course, before you can do anything clever like that, you have to
first know what happens to the partial differential equation when the
coordinates are changed. It turns out that the form of the
equation remains the same in the new coordinates:
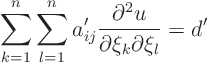
The expression for the new matrix ![]() can be written in either matrix
notation or index notation:
can be written in either matrix
notation or index notation:
The expression for the new right hand side ![]() is best written in
index notation:
is best written in
index notation:
Using equations (18.14) and (18.15) above, you
can figure out what the new matrix and right hand side are. However,
that may not yet be enough to fully transform the problem to the new
coordinates. Recall that the coefficients ![]() and
and ![]() might
involve first order derivatives with respect to
might
involve first order derivatives with respect to ![]() .
These derivatives must be converted to derivatives with respect to
.
These derivatives must be converted to derivatives with respect to
![]() . To do that, use:
. To do that, use:
That may still not be enough, because the resulting equation will
probably still contain ![]() themselves. You will also
need to express these in terms of
themselves. You will also
need to express these in terms of ![]() to get the
final partial differential equation completely in terms of the new
coordinates.
to get the
final partial differential equation completely in terms of the new
coordinates.
But that is it. You are now done. At least with the partial differential equation. There might also be boundary and/or initial conditions to invert. That can be done in a similar way, but we will skip it here.
One additional point should be made. If you follow the procedure as
outlined above exactly, you will have to express ![]() in terms of
in terms of ![]() , and differentiate these expressions.
You will also need to express
, and differentiate these expressions.
You will also need to express ![]() in terms of
in terms of
![]() to get rid of
to get rid of ![]() in the equations.
That is a lot of work. Also, if you are, say, switching from
Cartesian to sperical coordinates, the expressions for the spherical
coordinates in terms of the Cartesian ones are awkward. You would
much rather just deal with the expressions of the Cartesian
coordinates in terms of the spherical ones.
in the equations.
That is a lot of work. Also, if you are, say, switching from
Cartesian to sperical coordinates, the expressions for the spherical
coordinates in terms of the Cartesian ones are awkward. You would
much rather just deal with the expressions of the Cartesian
coordinates in terms of the spherical ones.
Now differentiating the ![]() with respect to the
with respect to the
![]() will give you matrix
will give you matrix ![]() instead of
instead of
![]() . But you can invert the matrix relatively easily using
the method of minors. While that is a bit of work, you also save a
lot of work because you no longer have to convert
. But you can invert the matrix relatively easily using
the method of minors. While that is a bit of work, you also save a
lot of work because you no longer have to convert ![]() in
the results to
in
the results to ![]() and clean up the mess.
and clean up the mess.
To convert ![]() into
into ![]() , as described above, you will need to
evaluate the second order derivatives of
, as described above, you will need to
evaluate the second order derivatives of ![]() in it.
Do that as
in it.
Do that as
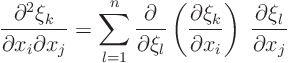
Derivation {D.4} gives the derivation of the various formulae above.
The purpose of this section is to simplify second order partial
differential equations by rotating the coordinate system to a
different orientation. This allows you to simplify the matrix ![]() of
the partial differential equation considerably. In particular, in
this way you can bring the new matrix
of
the partial differential equation considerably. In particular, in
this way you can bring the new matrix ![]() into the form of a
into the form of a
diagonal
matrix:
One limitation to the procedure in this section should be stated right
away. It concerns the case that the matrix ![]() is not constant, but
varies from point to point. For such a partial differential equation,
you can select a point, any point you like, and bring the equation in
the above diagonal form at that one selected point. At other
points there will then still be mixed derivatives in the transformed
equation.
is not constant, but
varies from point to point. For such a partial differential equation,
you can select a point, any point you like, and bring the equation in
the above diagonal form at that one selected point. At other
points there will then still be mixed derivatives in the transformed
equation.
To figure out how to convert a partial differential equation to
the above diagonal form, first a brief review of linear algebra is
needed. First recall that in three dimensions, you can define
basis vectors
![]()
![]()
![]() ,
, ![]()
![]()
![]() , and
, and ![]()
![]()
![]() . And you can write any other
three dimensional vector in terms of these three basis vectors, like
for example
. And you can write any other
three dimensional vector in terms of these three basis vectors, like
for example ![]() . Similarly in
. Similarly in ![]() dimensions you
can define
dimensions you
can define ![]() basis vectors
basis vectors ![]()
![]()
![]() ,
,
![]()
![]()
![]() , ...
, ...![]()
![]()
![]() .
.
Next, a simple linear transformation of coordinates (which leaves the
origin unchanged) takes the form, by definition,
Matrix ![]() consists of the
consists of the basis vectors
of the new
coordinate system, viewed from the old coordinate system. So for the
special case that the transformation is a simple rotation of the
coordinate system, matrix ![]() consists of the rotated basis vectors
consists of the rotated basis vectors
![]() , call them
, call them
![]() , viewed from the original
coordinate system. (Conversely,
, viewed from the original
coordinate system. (Conversely, ![]() consists of the original
basis vectors
consists of the original
basis vectors ![]() when viewed from the
new coordinate system.) The important thing to remember is that for
the special case of coordinate rotation, the inverse of
when viewed from the
new coordinate system.) The important thing to remember is that for
the special case of coordinate rotation, the inverse of ![]() is just
its transpose:
is just
its transpose:
Note further that for linear transformations, the Jacobian matrices
are just
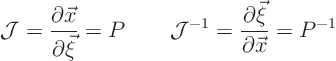
Now it is known from linear algebra that this becomes the diagonal
matrix ![]() given at the start of the subsection if you take
given at the start of the subsection if you take
![]() as the matrix
as the matrix ![]() of eigenvectors of
of eigenvectors of ![]() . (If
. (If ![]() varies from point to point, that means more specifically the
eigenvectors of the selected point.) But for a rotation of
coordinates,
varies from point to point, that means more specifically the
eigenvectors of the selected point.) But for a rotation of
coordinates, ![]()
![]()
![]() is just
is just ![]() . So the needed
coordinate transform is
. So the needed
coordinate transform is
Warning: you must normalize the eigenvectors (divide them by their
length) because the basis vectors ![]() are
all of length one. And first you must make sure every one is
orthogonal to all the others. Fortunately, that is normally
automatic. However, if you have a double eigenvalue, any two
corresponding eigenvectors are not necessarily orthogonal; you must
explicitly make them so. Similarly, for a triple eigenvalue, you will
need to create three corresponding orthogonal eigenvectors. And then
divide each by its length. (To check whether vectors are orthogonal,
check that their dot product is zero.)
are
all of length one. And first you must make sure every one is
orthogonal to all the others. Fortunately, that is normally
automatic. However, if you have a double eigenvalue, any two
corresponding eigenvectors are not necessarily orthogonal; you must
explicitly make them so. Similarly, for a triple eigenvalue, you will
need to create three corresponding orthogonal eigenvectors. And then
divide each by its length. (To check whether vectors are orthogonal,
check that their dot product is zero.)
Some books, like [3], do not bother to
normalize the eigenvectors to length one. In that case the coordinate
transformation is not just a rotation, but also a stretching of the
coordinate system. The matrix ![]() is still diagonal, but the values
on the main diagonal are no longer the eigenvalues of
is still diagonal, but the values
on the main diagonal are no longer the eigenvalues of ![]() . Also, it
becomes messier to find the old coordinates in terms of the new ones.
You would have to find the inverse of
. Also, it
becomes messier to find the old coordinates in terms of the new ones.
You would have to find the inverse of ![]() using minors. Using
orthonormal rather than just orthogonal eigenvectors is recommended.
using minors. Using
orthonormal rather than just orthogonal eigenvectors is recommended.
You might wonder, if ![]() varies from point to point, why can we not
simply set
varies from point to point, why can we not
simply set
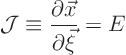
Do recall that you will also have to transform the right hand side ![]() to the new coordinates. However, the second formula in
(18.21) implies that the right hand side
to the new coordinates. However, the second formula in
(18.21) implies that the right hand side ![]() is the same in
the transformed equation as in the original one:
is the same in
the transformed equation as in the original one: ![]() are linear in
are linear in ![]() , so their second order derivatives in
(18.15) are zero.
, so their second order derivatives in
(18.15) are zero.
You will need the first formula in (18.21), in terms of its
components, to get rid of any coordinates ![]() in the
right hand side
in the
right hand side ![]() in favor of
in favor of ![]() . Also, if
. Also, if ![]() contains derivatives with respect to the unknowns
contains derivatives with respect to the unknowns ![]() ,
you will need to convert those using (18.16) of the
previous subsection. To get the derivatives
,
you will need to convert those using (18.16) of the
previous subsection. To get the derivatives ![]() with
respect to
with
respect to ![]() while doing so, write out the second
formula in (18.21) in terms of its components.
while doing so, write out the second
formula in (18.21) in terms of its components.
ExampleQuestion: Classify the equation
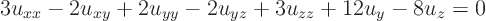
and put it in canonical form.Solution:
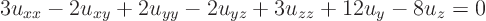
Identify the matrix:
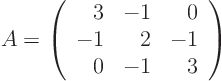
To find the new coordinates (transformation matrix), find the eigenvalues and eigenvectors of
:
The eigenvalues are the roots of
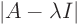
0:
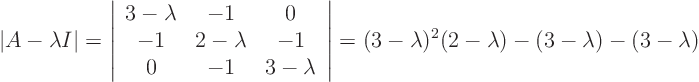
Hence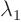
1,
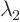
3,
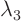
4.
The eigenvectors are solutions of
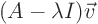
0 that are normalized to length one. For
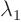
1, writing matrix
and applying Gaussian elimination on it produces
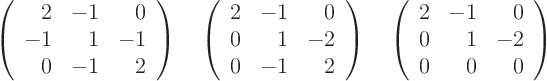
which gives the normalized eigenvector
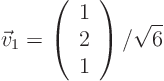
For
3,
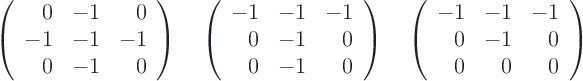
which gives the normalized eigenvector
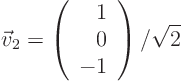
For
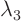
4,
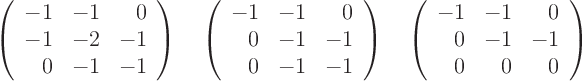
which gives the normalized eigenvector
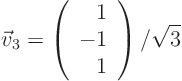
The new equation is:
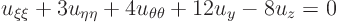
However, that still contains the old coordinates in the first order terms. Use the transformation formulae and total differentials to convert the first order derivatives:
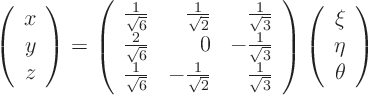
and its inverse
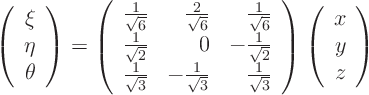
The partial derivatives of
with respect to
can be read off from the final matrix. So
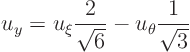
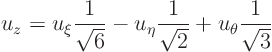
Hence in the rotated coordinate system, the partial differential equation is:
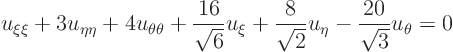
Simplify the partial differential equation
The previous subsection showed how partial differential equations can be simplified by rotating the coordinate system. Using this procedure it is possible to understand why second order partial differential equations are classified as described in section 18.6.2.
From the above, it already starts to become clearer why the
classification of second order partial differential equations is in
terms of the eigenvalues ![]() . If two different second order partial
differential equations have the same eigenvalues of their matrix
. If two different second order partial
differential equations have the same eigenvalues of their matrix ![]() ,
then you can simply rotate the coordinate system to make their
matrices
,
then you can simply rotate the coordinate system to make their
matrices ![]() equal. And the highest order derivatives make the
biggest difference for the physical behavior of the system. For
short-scale effects, which include singularities, the highest order
derivatives dominate. For them, the right hand side
equal. And the highest order derivatives make the
biggest difference for the physical behavior of the system. For
short-scale effects, which include singularities, the highest order
derivatives dominate. For them, the right hand side ![]() is relatively
unimportant. And since the highest order terms are now equal for the
two partial differential equations, they must behave very similarly.
So they should be classified as being in the same group.
is relatively
unimportant. And since the highest order terms are now equal for the
two partial differential equations, they must behave very similarly.
So they should be classified as being in the same group.
Rotation of the coordinate system reduces a partial differential
equation of the form
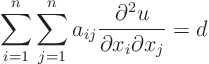
That immediately explains why only the eigenvalues of matrix ![]() are
of importance for the classification. Rotating the mathematical
coordinate system obviously does not make any difference for the
physical nature of the solutions. And in the rotated coordinates, all
that is left of matrix
are
of importance for the classification. Rotating the mathematical
coordinate system obviously does not make any difference for the
physical nature of the solutions. And in the rotated coordinates, all
that is left of matrix ![]() are its eigenvalues.
are its eigenvalues.
The next question is why the classification only uses the signs of the eigenvalues, not their magnitudes. The reason is that the magnitude can be scaled away by stretching the coordinates. That is demonstrated in the next example.
ExampleQuestion: The previous example reduced the elliptic partial differential equation
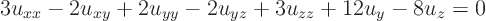
to the form
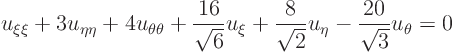
Reduce this equation further until it becomes as closely equal to the Laplace equation as possible.Solution:
The first step is to make the coefficients of the second order derivatives equal in magnitude. That can be done by stretching the coordinates. If
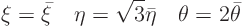
then
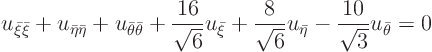
Note that all that is left in the second order derivative terms is the sign of the eigenvalues.
You can get rid of the first order derivatives by changing to a new independent variable
. To do so, set
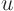

. Plug this into the differential equation above and differentiate out the product. Then choose
,
, and
so that the first derivatives drop out. You will find that you need:
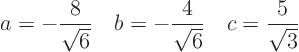
Then the remaining equation turns out to be:
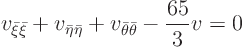
It is not exactly the Laplace equation because of the final term. But the final term does not even involve a first order derivative. It makes very little difference for short-scale phenomena. And short scale phenomena (such as singularities) are the most important for the qualitative behavior of the partial differential equation.
As this example shows, the values of the nonzero eigenvalues can be normalized to 1 by stretching coordinates. However, the sign of the eigenvalues cannot be changed. And neither can you change a zero eigenvalue into a nonzero one, or vice-versa, by stretching coordinates.
You might wonder why all this also applies to partial differential
equations that have variable coefficients ![]() and
and ![]() . Actually,
what
. Actually,
what ![]() is does not make much of a difference. But generally
speaking, rotation of the coordinate system only works if the
coefficients
is does not make much of a difference. But generally
speaking, rotation of the coordinate system only works if the
coefficients ![]() are constant. If they depend on position, the
eigenvectors
are constant. If they depend on position, the
eigenvectors ![]() at every point can still be
found. So it might seem logical to try to find the new coordinates
at every point can still be
found. So it might seem logical to try to find the new coordinates
![]() from solving
from solving
![]()
![]()
![]() . But
the problem is that that are
. But
the problem is that that are ![]() equations for only
equations for only ![]() unknown
coordinates. If the unit vectors are not constant, these equations
normally mutually conflict and cannot be solved.
unknown
coordinates. If the unit vectors are not constant, these equations
normally mutually conflict and cannot be solved.
The best that can normally be done for arbitrary ![]() is to select a
single point that you are interested in. Then rotate the coordinate
system to diagonalize the partial differential equation at that one
point. In that case,
is to select a
single point that you are interested in. Then rotate the coordinate
system to diagonalize the partial differential equation at that one
point. In that case, ![]() is diagonal near the considered point. And
that is enough to classify the equation at that point. For, the most
important feature that the classification scheme tries to capture is
what happens to short scale phenomena. Short scale phenomona will
is diagonal near the considered point. And
that is enough to classify the equation at that point. For, the most
important feature that the classification scheme tries to capture is
what happens to short scale phenomena. Short scale phenomona will
see
the locally diagonal equation. So the
classification scheme continues to work.
Convert the equation