|
|
|
|
|
Next: A.23 Quantization of radiation |
|
As noted in chapter 7.5.2, the fundamental forces of nature
arise from the exchange of particles. This addendum will illustrate
the general idea. It will first derive the hypothetical
Koulomb
force due to the exchange of equally
hypothetical particles called fotons.
The Koulomb potential provides a fairly simple model of a quantum field. It also provides a simple context to introduce some key concepts in quantum field theories, such as Green’s functions, variational calculus, Lagrangians, the limitation of the speed of light, description in terms of momentum modes, Fock space kets, annihilation and creation operators, antiparticles, special relativity, the imperfections of physicists, and Lorentz invariance. The Koulomb potential can also readily be modified to explain nuclear forces. However, that will have to wait until a later addendum, {A.42}.
In the current addendum, the Koulomb potential provides the starting point for a discussion of the electromagnetic field. The classical Maxwell equations for the electromagnetic field will be derived in a slightly unconventional way. Who needs to know classical electromagnetics when all it takes is quantum mechanics, relativity, and a few plausible guesses to derive electromagnetics from scratch?
To quantize the electromagnetic field is not that straightforward; it has unexpected features that do not occur for the Koulomb field. This book follows the derivation as formulated by Fermi in 1932. This derivation is the basis for more advanced modern quantum field approaches. These advanced theories will not be covered, however.
Essentially, the Fermi derivation splits off the Coulomb potential from the electromagnetic field. What is left is then readily described by a simple quantum field theory much like for the Koulomb potential. This is sufficient to handle important applications such as the emission or absorption of radiation by atoms and atomic nuclei. That, however, will again be done in subsequent addenda.
A word to the wise. While this addendum is on the calculus level like virtually everything else in this book, there is just quite a lot of mathematics. Some mathematical maturity may be needed not to get lost. Note that this addendum is not needed to understand the discussion of the emission and absorption of radiation in the subsequent addenda.
The Koulomb force holds the sarged spotons and selectons together in satoms. The force is due to the exchange of massless particles called fotons between the sarged particles. (It will be assumed that the spoton is an elementary particle, though really it consists of three skarks.)
This subsection will derive the selectostatic Koulomb force by representing the fotons by a classical field, not a quantum field. The next subsection will explain classical selectodynamics, and how it obeys the speed of light. Subsection A.22.3 will eventually fully quantize the selectic field. It will show how quantum effects modify some of the physics expected from the classical analysis.
Physicists have some trouble measuring the precise properties of the selectic field. However, a few basic quantum ideas and some reasonable guesses readily substitute for the lack of empirical data. And guessing is good. If you can guess a self-consistent Koulomb field, you have a lot of insight into its nature.
Consider first the wave function for the exchanged foton in isolation.
A foton is a boson without spin. That means that its wave function is
a simple function, not some vector. But since the foton is massless,
the Schrödinger equation does not apply to it. The appropriate equation
follows from the relativistic expression for the energy of a massless
particle as given by Einstein, chapter 1.1.2
(1.2):
Quantum mechanics replaces the momentum vector by the operator
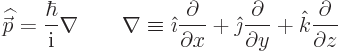
nablaor
del.This operator is treated much like an ordinary vector in various computations. Its properties are covered in Calculus III in the U.S. system. (Brief summaries of properties of relevance here can be found in the notations section.)
The Hamiltonian eigenvalue problem for a foton wave function
![]()
Using the momentum operator as given above and some rearranging, the
eigenvalue problem becomes
For foton wave functions that are not necessarily energy eigenstates,
quantum mechanics replaces the energy ![]()
![]()
![]()
![]() .
.
Now consider solutions of this equation of the form
Planck-Einsteinrelation. It is implicit in the association of
Note however that there will also be a solution of the form
antiparticle.So the wave function above describes an
antifoton.
There is really no physical difference between a foton and an antifoton. That is not necessarily true for other types of particles. Quantities such as electric charge, lepton number, baryon number, strangeness, etcetera take opposite values for a particle and its antiparticle.
There is a very important difference between the Klein-Gordon equation
and the Schrödinger equation. The Schrödinger equation describes nonrelativistic
physics where particles can neither be destroyed nor created. Mass
must be conserved. But the Klein-Gordon equation applies to
relativistic physics. In relativistic physics particles can be
created out of pure energy or destroyed following Einstein’s
famous relationship ![]()
![]()
![]() ,
,
There is a mathematical consequence to this. It concerns the integral
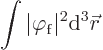
But fotons are routinely destroyed or created by sarged particles. So
the probability of finding a foton is not a preserved quantity. (It
is not even clear what finding a foton would mean in the first place.)
The Klein-Gordon equation reflects that. It does not preserve the
integral ![]() .
.
But the Klein-Gordon equation does preserve an other integral,
{D.32}. That is
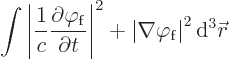
Now if the number of fotons is not a preserved quantity, what can this preserved integral stand for? Not momentum or angular momentum, which are vectors. The integral must obviously stand for the energy. Energy is still preserved in relativity, even if the number of particles of a given type is not.
Of course, the energy of a foton wave function ![]()
![]() ,
,
And if there is an observable field, there must be an observable
energy associated with that field. Now what could the expression for
the energy in the field be? Obviously it will have to take the form
of the integral above. What other options are there that are
plausible? Of course, there will be some additional empirical
constant. If the integral is constant, then any multiple of it will
be constant too. And the above integral will not have units of energy
as it is. The needed empirical constant is indicated by ![]()
That is really all that is needed to figure out the properties of classical selectostatics in this subsection. It will also be enough to figure out classical selectodynamics in the next subsection.
The first system that will be considered here is that of a foton field
and a single spoton. It will be assumed that the spoton is pretty
much located at the origin. Of course, in quantum mechanics a
particle must have some uncertainty in position, or its kinetic energy
would be infinite. But it will be assumed that the spoton wave
function is only nonzero within a small distance ![]()
However, since this is a classical derivation and not a quantum one,
the term spoton wave function
must not be used. So
imagine instead that the spoton sarge ![]()
![]()
For a smeared out sarge, there will be a sarge density
![]() ,
,
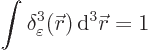
In the limit that ![]()
![]()
![]() .
.
Here the big question is how the spoton manages to create a foton
field around itself. That is not trivial. If there was a nonzero
probability of finding an energetic foton well away from the spoton,
surely it would violate energy conservation. However, it turns out
that the time-independent Klein-Gordon equation (A.101)
actually has a very simple solution where the foton energy ![]()
This then seems to be a plausible form for the observable potential
![]()
![]()
![]()
![]()
All that then raises the question why there is a foton field in the
first place. The interest in this subsection is in the selectostatic
field. That is supposed to be the stable ground state of lowest
energy. According to the above, the state of lowest energy would be
when there is no foton field; ![]()
![]()
And so it is. The only reasonable way to explain that there is a nontrivial foton field in the ground state of the spoton-foton system is if the foton field energy is compensated for by something else. There must be an energy of interaction between the foton field and the spoton.
Consider the mathematical form that this energy could take in a given
volume element ![]() .
.![]()
![]() .
.
The question is now, what is the ground state foton field? In other
words, for what potential ![]()
Suppose that you wanted an equation for the minimum of some function
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() :
:
It is the same for the change in net energy
![]() .
.![]()
![]()
![]()
![]() .
.![]() :
:![]()
![]() .
.![]()
So the requirement for the ground state potential is
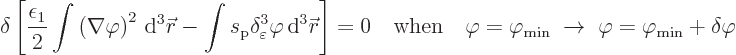
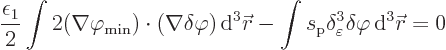
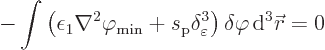
The parenthetical expression can now be rearranged to give the final
result:
minwas left away again as the ground state is the only state of interest here anyway.
The above equation is the famous “Poisson equation” for the selectostatic potential
![]() .
.forcing
term; it
forces a nonzero solution for ![]() .
.
Beyond the small vicinity of radius ![]()
![]()
![]()
For unit value of ![]()
![]()
![]()
If the spoton is not at the origin, but at some position
![]() ,
,![]()
Now the net energy is of interest. It can be simplified by
substituting the Poisson equation (A.106) in the expression
(A.104) for the foton field energy and adding the interaction
energy (A.105). That gives
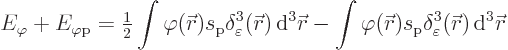
The fact that there is a foton field in the ground state has now been explained. The interaction with the spoton lowers the energy more than the field itself raises it.
Note further from the solution for ![]()
![]()
The final step to derive the classical Koulomb force is to add a
selecton. The selecton is also sarged, so it too generates a field.
To avoid confusion, from now on the field generated by the spoton will
always be indicated by ![]() ,
,![]() .
.
All three effects turn out to produce the same energy, but the first
two energies are negative and the third positive. So the net energy
change is the same as if there was just item 1, the interaction of the
selecton sarge density ![]()
![]()
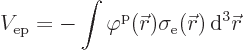
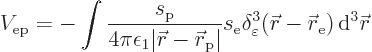
Since ![]()
![]() .
.![]()
![]()
That then is the final energy of the Koulomb interaction between the two sarged particles. Because the spoton and the selecton both interact with the foton field, in effect it produces a spoton-selecton interaction energy.
Of course, in classical physics you would probably want to know the
actual force on say the selecton. To get it, move the origin of the
coordinate system to the spoton and rotate it so that the selecton
is on the positive ![]() -
-![]()
![]() -
-![]()
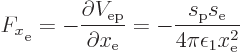
More generally, the force on the selecton points towards the spoton if the sarges are of the same sign. It points straight away from the spoton if the sarges are of opposite sign.
The Koulomb energy ![]()
Now a spoton must necessarily create a foton field that is attractive to spotons. Otherwise there should be no field at all in the ground state. And if spotons create fields that attract spotons, then spotons attract. So the Koulomb force is clearly right.
It is the Coulomb force that does not seem to make any sense. Much more will be said about that in later subsections.
According to the previous section the Koulomb energy between a spoton
and a selecton is given by
To see the problem, imagine that the spoton is suddenly given a kick. According to the Koulomb potential given above, the selecton notices that instantly. There is no time in the Koulomb potential, so there is no time delay. But Einstein showed that no observable effect can move faster than the speed of light. So there should be a time delay.
Obviously then, to discuss unsteady evolution will require the full governing equations for selectodynamics. The big question is how to find these equations.
The quantum mechanics in this book is normally based on some
Hamiltonian ![]() .
.![]() .
.
To get at the Lagrangian for selectodynamics, consider first the
motion of the spoton for a given foton field ![]() .
.
However, to discuss the dynamics of the spoton, it is easier to
consider it a point particle located at a single moving point
![]() .
.![]() .
.![]() .
.
In addition to the interaction energy above there is the kinetic
energy of the spoton,
Now the Hamiltonian of the spoton is the sum of the kinetic and
potential energies. But the Lagrangian is the difference
between the kinetic and potential energies:
This Lagrangian can now be used to find the equation of motion of the
spoton. This comes about in a somewhat weird way. Suppose that there
is some range of times, from a time ![]()
![]() ,
,![]()
![]() .
.action
integral
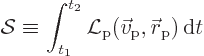
Probably this sounds like a stupid mathematical trick. But in the so-called path integral approach to quantum field theory, the action is central to the formulation.
For classical physics the action by itself is pretty useless.
However, with some manipulations, you can get the evolution equations
for your system out of it, {A.1}. They are found
as
Note that for the governing equations it does not matter at all what
you take the times ![]()
![]()
The next step is to write out the governing equation (A.112)
in terms of physical quantities. To do that correctly, the trick is
that the Lagrangian must be treated as a function of velocity and
position, as independent variables. In reality velocity and position
are not independent; velocity is the derivative of position. But when
differentiating the Lagrangian you are supposed to forget about that.
Consider how this works out for the ![]() -
-![]()
![]()
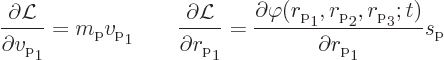
However, when you do the remaining time derivative in (A.112)
you have to do it properly, treating the velocity as the function of
time that it is. That gives the final equation of motion as
Note that the left hand side is mass times acceleration in the
![]() -
-Sorentz force.
It is seen that the Sorentz force is proportional to the derivative of
the foton potential, evaluated at the position of the spoton. If you
compare the Sorentz force with the force in electrostatics, you see
that the force in electrostatics has an additional minus sign. That
reflects again that equal sarges attract, while equal charges repel.
So far, it was assumed that the foton field was given. But in reality
the foton field is not given, it depends on the motion of the spoton.
To describe the field, its energies must be added to the Lagrangian
too. The total energy in the foton field was given in the previous
subsection as (A.103). Using some shorthand notation, this
becomes
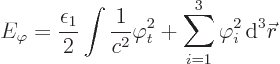
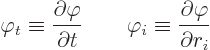
Actually, even more concise shorthand will be used. If an index like
![]()
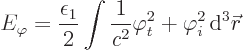
Now the first term in the energy above is a time derivative, just like
![]()
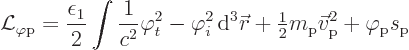
However, for the final term it is now desirable to go back to the
representation of the spoton in terms of a sarge density
![]() ,
,
An integrand of a spatial integral in a Lagrangian is called a
“Lagrangian density” and indicated by the symbol ![]() .
.
The action principle can readily be extended to allow for Lagrangian
densities, {D.37}. The equations of motion for the field
are then found to be
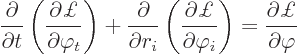
Working this out much like for the equation of motion of the spoton
gives, taking ![]()
Saxwell wave equationof selectodynamics. If there is also a selecton, say, its sarge density can simply be added to the spoton one in the right hand side.
To check the Saxwell equation, first consider the case that the system
is steady, i.e. independent of time. In that case the Saxwell wave
equation becomes the Poisson equation of the previous subsection as it
should. (The second term is summed over the three Cartesian
directions ![]() .
.![]() .
.
How about the force on a selecton in this field? Of course, the
force on a selecton is a Sorentz force of the same form as
(A.113),
self-interactionproduces no net force. That is fortunate because if the selecton was really a point sarge, the self-interaction is mathematically singular.) Now minus the potential (A.107) times the selecton sarge
So in the steady case the Saxwell equation combined with the Sorentz force does reproduce selectostatics correctly. That means that the given Lagrangian (A.114) contains all of selectostatics in a single concise mathematical expression. At the minimum. Neat, isn’t it?
Consider next the case that the time dependence cannot be ignored.
Then the time derivative in the Saxwell equation (A.116)
cannot be ignored. In that case the left hand side in the equation is
the complete unsteady Klein-Gordon equation. Since there is a nonzero
right-hand side, mathematically the Saxwell equation is an
inhomogeneous Klein-Gordon equation. Now it is known from the theory
of partial differential equations that the Klein-Gordon equation
respects the speed of light. As an example, imagine that at time ![]()
![]()
It follows that selectodynamics, as described by the Lagrangian (A.114), also respects the speed of light limitation.
The previous subsections derived the Koulomb force between sarged
particles. This force was due to foton exchange. While the
derivations used some ideas from quantum mechanics, they were
classical. The effect of the fotons took the form of a potential
![]()
![]() .
.![]()
observed
by a sarged spoton or
selecton.
However, that very fact violates the fundamental postulates of quantum mechanics as formulated at the beginning of this book, chapter 3.4. Observable values should be the eigenvalues of Hermitian operators that act on wave functions. While the foton potential was loosely associated with a foton wave function, wave functions should not be observable.
Now if classically every position has its own observable local
potential ![]() ,
,![]() .
.![]()
quantum field;
an infinite amount of operators, one
for each position.
The objective in this subsection is to deduce the form of this quantum field. And the type of wave function that it operates on. The results will then be used to verify the Koulomb force between stationary sarges as found the first subsection. It is imperative to figure out whether like sarges still attract in a proper quantum description.
Doing this directly would not be easy. It helps a lot if the field is written in terms of linear momentum eigenstates.
In fact, typical quantum field theories depend very heavily on this trick. However, often such theories use relativistic combined energy-momentum states in four-dimensional space-time. This subsection will use simpler purely spatial momentum states. The basic idea is the same. And it is essential for understanding the later Fermi derivation of the Coulomb potential.
Linear momentum states are complex exponentials of the form
![]() .
.![]()
![]()
![]()
![]() .
.![]()
If a field ![]()
![]()
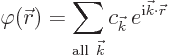
The expression above assumes that the entire system is confined to a very large periodic box, as in chapter 6.17. In infinite space the sum becomes an integral, section 7.9. That would be much more messy. (But that is the way you will usually find it in a typical quantum field analysis.) The precise values of the wave number vectors to sum over for a given periodic box were given in chapter 6.18 (6.28); they are all points in figure 6.17.
The first subsection found the selectostatic potential
![]()
According to the first subsection, the classical potential was the
solution to a Poisson equation; a steady Klein-Gordon equation with
forcing by the spoton:
clhas been added. Also note that since this is a now a quantum description, the spoton sarge density
Now the classical potential is to be written in the form
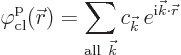
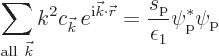
Now multiply this equation at both sides by some sample
complex-conjugate momentum eigenfunction ![]()
![]()
![]()
![]()
![]()
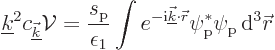
This solution is definitely one to remember. Note in particular that
the coefficients of the momentum states are a constant divided by
![]() .
.![]()
![]()
![]() ,
,
If the requirement that the spoton wave function is completely at the
origin is relaxed, the integral involving the spoton wave function
stays:
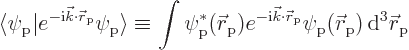
Now the objective is to reproduce this classical result using a proper quantum field theory. And to find the force when a selecton is added to the system.
To do so, consider initially a system of fotons and a single spoton.
The spoton will be treated as a nonrelativistic particle. Then its
wave function ![]()
Next the fotons. Their description will be done based upon linear
momentum states. Such a state corresponds to a single-foton wave
function of the form ![]() .
.
To keep it simple, for now only a single momentum state will be
considered. In other words, only a single wave number vector ![]()
Of course, at the end of the day the results must still be summed over
all values of ![]() .
.
Some notations are needed now. A situation in which there are no
fotons in the considered state will be indicated by the “Fock
space ket” ![]() .
.![]() ,
,![]() ,
,
The ground state wave function for the combined spoton-fotons system
is then assumed to be of the form
(It may be noted that in typical quantum field theories, a charged
relativistic particle would also be described in terms of kets and
some quantum field ![]() .
.![]()
![]()
observe
the particle. That resembles the Born
interpretation of the nonrelativistic wave function somewhat,
especially for a spinless particle. Compare [[17, pp. 49, 136, 144]]. The field ![]()
![]()
Now, of course, the Hamiltonian is needed. The Hamiltonian determines
the energy. It consists of three parts:
The second part is the Hamiltonian of the free foton field. Each
foton in the considered state should have an energy ![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() ,
,
Finally, the third part of the total Hamiltonian is the interaction
between the spoton and the foton field. This is the tricky one.
First recall the classical expression for the interaction energy.
According to the previous subsection, (A.111), it was
![]() .
.![]()
In quantum field theory, the observable field ![]()
![]() .
.
| (A.124) |
To answer that, first note that sarged particles can create and destroy fotons. The above interaction Hamiltonian must express that somehow. After all, it is the Hamiltonian that determines the time evolution of systems in quantum mechanics.
Now in quantum field theories, creation and destruction of particles
are accounted for through creation and annihilation operators,
{A.15}. A creation operator ![]()
![]() .
.![]()
Note incidentally that the foton field Hamiltonian given earlier can
now be rewritten as
But surely, the creation and annihilation of particles should also
depend on where the spoton is. Fotons in the considered state have a
spatially varying wave function. That should be reflected in the
quantum field ![]()
In those terms, the needed quantum field turns out to be
You might of course wonder about that second term. Mathematically it
is needed to make the operator Hermitian. Recall that operators in
quantum mechanics need to be Hermitian to ensure that observable
quantities have real, rather than complex values, chapter
2.6. To check whether an operator is Hermitian, you need
to check that it is unchanged when you take it to the other side of an
inner product. Now the wave function is a numerical quantity that
changes into its complex conjugate when taken to the other side. And
![]()
![]()
![]()
But what to make physically of the two terms? One way of thinking
about it is that the observed field is real because it does not just
involve an interaction with an ![]()
![]()
In general, the quantum field above would still need to be summed over
all wave numbers ![]() .
.![]()
![]()
![]()
![]() ,
,
With the quantum field ![]()
Note that the spoton has uncertainty in position. The spoton position in the Hamiltonian above is just a possible spoton position. In usage it will still get multiplied by the square spoton wave function magnitude that gives the probability for that position. Still, at face value the interaction of the spoton with the field takes place at the location of the spoton. Interactions in quantum field theories are “local.” At least on macroscopic scales that is needed to satisfy the limitation of the speed of light.
Having a Hamiltonian allows quantum selectodynamics to be explored. That will be done to some detail for the case of the electromagnetic field in subsequent addenda. However, here the only question that will be addressed is whether classical selectostatics as described in the first subsection was correct. In particular, do equal sarges still attract in the quantum description?
Selectostatics of the spoton-fotons system should correspond to the
ground state of the system. The ground state has the lowest possible
energy. You can therefore find the ground state by finding the state
of lowest possible system energy. That is the same trick as was used
to find the ground states of the hydrogen molecular ion and the
hydrogen molecule in chapters 4.6 and 5.2. The
expectation value
of the system energy is defined by
the inner product
Now to find the ground state, the lowest possible value of the
expectation energy above is needed. To get that, the inner products
between the kets in the factors ![]()
![]() ,
,
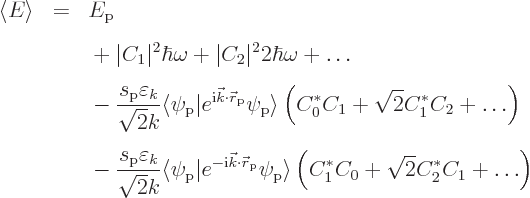
Note that the first term in the right hand side above is the energy
![]()
![]()
![]()
If the spoton sarge is nonzero however, the interaction terms in the
last two lines can lower the energy for suitable nonzero values of the
constants ![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
Further, since any complex number may always be written as its
magnitude times some exponential of magnitude 1, the second last
line of the energy above can be written as
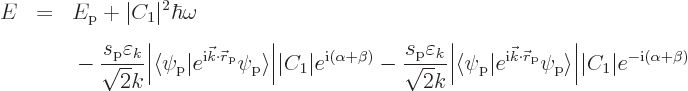
That still leaves the magnitude ![]()
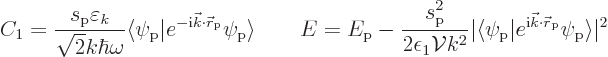
This energy-lowering still needs to be summed over all states ![]()
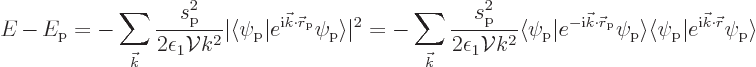
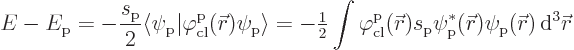
However now an actual picture of the quantum ground state has been obtained. It is a quantum superposition of system states. The most likely state is the one where there are no fotons at all. But there are also small probabilities for system states where there is a single foton in a single linear momentum foton state. This picture does assume that the spoton sarge is small. If that was not true, things would get much more difficult.
Another question is whether the observable values of the foton potential are the same as those obtained in the classical analysis. This is actually a trick question because even the classical foton potential is not observable. There is still an undetermined constant in it. What is observable are the derivatives of the potential: they give the observable selectic force per unit sarge on sarged particles.
Now, in terms of momentum modes, the derivatives of the classical
potential can be found by differentiating (A.119). That gives
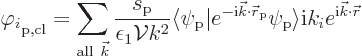
The question is now whether the quantum analysis predicts the same observable forces. Unfortunately, the answer here is no. The observable forces have quantum uncertainty that the classical analysis missed. However, the Ehrenfest theorem of chapter 7.2.1 suggests that the expectation forces should still match the classical ones above.
The quantum expectation force per unit sarge in the
![]() -
-
The above expression can be multiplied out as before. Using the
obtained expression for ![]() ,
,![]()
![]()
To see that there really is quantum uncertainty in the forces, it
suffices to look at the expectation square forces. If there
was no uncertainty in the forces, the expectation square forces would
be just the square of the expectation forces. To see that that is not
true, it is sufficient to simply take the spoton sarge zero. Then
the expectation field is zero too. But the expectation square field
is given by
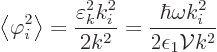
The above expression can be compared with the corresponding
![]()
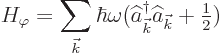
The bad news is that if you sum these ground state energies over all
values of ![]() ,
,
The final issue to be addressed is the attraction between a spoton and a selecton. That can be answered by simply adding the selecton to the spoton-fotons analysis above, {D.37.2}. The answer is that the spoton-selecton interaction energy is the same as found in the classical analysis.
So equal sarges still attract.
The Koulomb universe is a grim place. In selectodynamics, particles with the same sarge attract. So all selectons clump together into one gigantic ball. Assuming that spotons have the opposite sarge, they clump together into another big ball at the other end of the universe. But actually there is no justification to assume that spotons would have a different sarge from selectons. That then means that all matter clumps together into a single gigantic satom. A satom like that will form one gigantic, obscene, black hole. It is hardly conductive to the development of life as we know it.
Unfortunately, the Koulomb force is based on highly plausible, apparently pretty unavoidable assumptions. The resulting force simply makes sense. None of these things can be said about the Coulomb force.
But maybe, just maybe, the Koulomb juggernaut can be tripped up by some legal technicality. Things like that have happened before.
Now in a time not really that very long ago, there lived a
revolutionary of mathematics called Poincaré. Poincaré dreamt of
countless shining stars that would sweep through a gigantic, otherwise
dark universe. And around these stars there would be planets
populated by living beings called observers.
But if
the stars all moved in random directions, with random speeds, then
which star would be the one at rest? Which star would be the king
around which the other stars danced? Poincaré thought long and hard
about that problem. No!
he thundered eventually;
“It shall not be. I hereby proclaim that all stars are created
equal. Any observer at any star can say at any given time that its
star is at rest and that the other stars are moving. On penalty of
dead, nothing in physics may indicate that observer to be
wrong.”
Now nearby lived a young physicist called Einstein who was very lazy. For example, he almost never bothered to write the proper summation symbols in his formulae. Of course, that made it difficult for him to find a well paying job in some laboratory where they smash spotons into each other. Einstein ended up working in some patent office for little pay. But, fortunate for our story, working in a patent office did give Einstein a fine insight in legal technicalities.
First Einstein noted that the Proclamation of Poincaré meant that observers at different stars had to disagree seriously about the locations and times of events. However, it would not be complete chaos. The locations and times of events as perceived by different observers would still be related. The relation would be a transformation that the famous physicist Lorentz had written down earlier, chapter 1.2.1 (1.6).
And the Proclamation of Poincaré also implied that different observers had to agree about the same laws of physics. So the laws of physics should remain the same when you change them from one observer to the next using the Lorentz transformation. Nowadays we would say that the laws of physics should be “Lorentz invariant.” But at the time, Einstein did not want to use the name of Lorentz in vain.
Recall now the classical action principle
of
subsection A.22.2. The so-called action integral had to be
unchanged under small deviations from the correct physics. The
Proclamation of Poincaré demands that all observers must agree that
the action is unchanged. If the action is unchanged for an observer
at one star, but not for one at another star, then not all stars are
created equal.
To see what that means requires a few fundamental facts about special relativity, the theory of systems in relative motion.
The Lorentz transformation badly mixes up spatial positions and times
of events as seen by different observers. To deal with that
efficiently, it is convenient to combine the three spatial coordinates
and time into a single four-dimensional vector, a four-vector, chapter
1.2.4. Time becomes the “zeroth
coordinate” that joins the three spatial coordinates. In
various notations, the four-vector looks like
![\begin{displaymath}
\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspa...
...\ \strut x^3\end{array}\right)
\equiv
\{x^\mu\}
\to
x^\mu
\end{displaymath}](img4563.gif)
However, in virtually any quantum field book, you will find
four-vectors indicated by ![]() .
.![]()
![]()
![]() ,
,![]() .
.![]()
![]() .
.![]()
![]() ;
;
There are similar notations for the derivatives of a function
![]() :
:
![\begin{displaymath}
\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspa...
...array}\right)
\equiv
\{\partial_\mu f\}
\to
\partial_\mu f
\end{displaymath}](img4567.gif)
Quantum field books use ![]()
![]()
![]()
![]() .
.
The final key fact to remember about special relativity is:
In dot products between four-vectors, the product of the zeroth components gets a minus sign.Dot products between four-vectors are very important because all observers agree about the values of these dot products. They are Lorentz invariant. (In nonrelativistic mechanics, all observers agree about the usual dot products between spatial vectors. That is no longer true at relativistic speeds.)
One warning. In almost all modern quantum field books, the products
of the spatial components get the minus sign instead of the
time components. The purpose is to make the relativistic dot product
incompatible with the nonrelativistic one. After all,
backward compatibility
is so, well, backward. (One
source that does use the compatible dot product is [49].
This is a truly excellent book written by a Nobel Prize winning
pioneer in quantum field theory. It may well be the best book on the
subject available. Unfortunately it is also very mathematical and the
entire thing spans three volumes. Then again, you could certainly
live without supersymmetry.)
One other convention might be mentioned. Some books put a factor
![]()
![]()
![]()
Armed with this knowledge about special relativity, the Koulomb force
can now be checked. Action is defined as
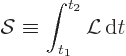
If all observers agree about the value of the action in
selectodynamics, then selectodynamics is Lorentz invariant. Now the
Lagrangian of classical selectodynamics was of the form, subsection
A.22.2,
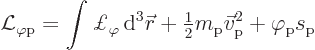
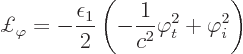
Note that the parenthetical term in the Lagrangian density is simply
the square of the four-vector of derivatives of ![]() .
.
To be sure, it is the action and not the Lagrangian density that must
be Lorentz invariant. But note that in the action, the Lagrangian
density gets integrated over both space and time. Such integrals are
the same for any two observers. You can easily check that from the
Lorentz transformation chapter 1.2.1 (1.6) by
computing the Jacobian of the ![]()
(OK, the limits of integration are not really the same for different observers. One simple way to get around that is to assume that the field vanishes at large negative and positive times. Then you can integrate over all space-time. A more sophisticated argument can be given based on the derivation of the action principle {A.1.5}. From that derivation it can be seen that it suffices to consider small deviations from the correct physics that are localized in both space and time. It implies that the limits of integration in the action integral are physically irrelevant.)
(Note that this subsection does no longer mention periodic boxes. In relativity periodicity is not independent of the observer, so the current arguments really need to be done in infinite space.)
The bottom line is that the first, integral, term in the Lagrangian produces a Lorentz-invariant action. The second term in the Lagrangian is the nonrelativistic kinetic energy of the spoton. Obviously the action produced by this term will not be Lorentz invariant. But you can easily fix that up by substituting the corresponding relativistic term as given in chapter 1.3.2. So the lack of Lorentz invariance of this term will simply be ignored in this addendum. If you want, you can consider the spoton mass to be the moving mass in the resulting equations of motion.
The final term in the Lagrangian is the problem. It represents the
spoton-fotons interaction. The term by itself would be Lorentz
invariant, but it gets integrated with respect to time. Now in
relativity time intervals ![]()
(To be sure, any good lawyer would have pointed out that there is no
problem if the spoton sarge density, instead of the spoton sarge
![]() ,
,
The question is now of course how to fix this up. That will hopefully
produce a more appealing universe. One in which particles like
protons and electrons have charges ![]()
![]() .
.
Consider the form of the problem term in the Koulomb action:
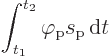
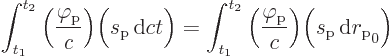
But the photon potential must also become a four-vector, instead of a
scalar. That is what it takes to achieve Lorentz invariance. So
electrodynamics defines a four-vector of potentials of the form
![\begin{displaymath}
{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}...
...\ \strut A^3\end{array}\right)
\equiv
\{A^\mu\}
\to
A^\mu
\end{displaymath}](img4578.gif)
vector potentialwhile
The interaction term in the action now becomes, replacing the spoton
sarge ![]()
![]() ,
,
![\begin{displaymath}
\int_{t_1}^{t_2} {\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hb...
...ace{0pt}}}\over r}
\kern-1.3pt_{\rm {p}}}{{\rm d}t} { \rm d}t
\end{displaymath}](img4580.gif)
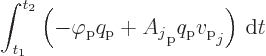
The integrand above is the interaction term in the electromagnetic
Lagrangian,
The Lagrangian density of the photon field is also needed. Since
the photon field is a four-vector rather than a scalar, the
self-evident electromagnetic density is
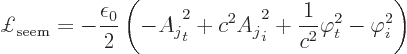
It might be noted that in principle the proper Lagrangian density could be minus the above expression. But a minus sign in a Lagrangian does not change the motion. The convention is to choose the sign so that the corresponding Hamiltonian describes energies that can be increased by arbitrarily large amounts, not lowered by arbitrarily large amounts. Particles can have unlimited amounts of positive kinetic energy, not negative kinetic energy.
Still, it does seem worrisome that the proper sign of the Lagrangian density is not self-evident. But that issue will have to wait until the next subsection.
Collecting things together, the self-evident Lagrangian for
electromagnetic field plus proton is
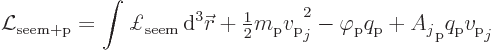
The first thing to check now is the equation of motion for the proton.
Following subsection A.22.2, it can be found from
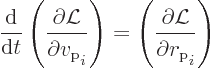
This can be cleaned up, {D.6}. In short, first an
electric” field
field ![]()
![]()
Lorentz force.
Note that there are 4 potentials with 4 derivatives each, for a
total of 16 derivatives. But matter does not observe all 16
individually. Only the 3 components of the electric field and the 3
of the magnetic field are actually observed. That suggests that there
may be changes to the fields that can be made that are not observable.
Such changes are called gage (or gauge) changes.
The
name arises from the fact that a gage is a measuring device. You and
I would then of course say that these changes should be called
nongage changes. They are not measurable. But
gage
is really shorthand for “Take that, you
stupid gage.”
Consider the most general form of such gage changes. Given potentials
![]()
![]() ,
,
The potentials ![]()
![]()
![]()
![]() .
.
The fact that you can make unmeasurable changes to the potentials like
that is called the gage
(or gauge) property of the
electromagnetic field. Nonphysicists probably think it is something
you read off from a voltage gage. Hilarious, isn’t it?
Observable or not, the evolution equations of the four potentials are
also needed. To find them it is convenient to spread the proton
charge out a bit. That is the same trick as was used in subsection
A.22.2. For the spread-out charge, a “charge
density” ![]()
![]()
The interaction terms can now be included in the Lagrangian density to
give the total Lagrangian
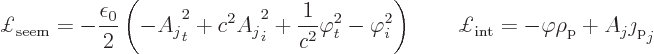
The field equations now follow similarly as in subsection
A.22.2. For the electrostatic potential:
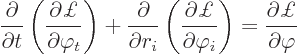
Similarly, for the components of the vector potential
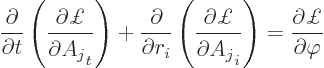
The above equations are again Klein-Gordon equations, so they respect the speed of light. And since the action is now Lorentz invariant, all observers agree with the evolution. That seems very encouraging.
Consider now the steady case, with no charge motion. The current
density ![]()
The steady equation (A.135) for the electrostatic field
![]()
But wait a second. How come that apparently protons suddenly manage to create fields that are repulsive to protons? What happened to energy minimization? It seems that all is not yet well in the universe.
The previous subsection derived the self-evident equations of electromagnetics. But there were some worrisome aspects. A look at the Hamiltonian can clarify the problem.
Given the Lagrangian (A.134) of the previous subsection, the
Hamiltonian can be found as, {A.1.5}:
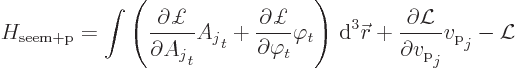
Note that the electrostatic potential ![]()
![]() .
.
That then answers the question of the previous subsection: “How come a proton produces an electrostatic field that repels it? What happened to energy minimization?” There is no such thing as energy minimization here. If there is no lowest energy, then there is no ground state. Instead the universe should evolve towards larger and larger electrostatic fields. That would release infinite amounts of energy. It should blow life as we know it to smithereens. (The so-called second law of thermodynamics says, simply put, that thermal energy is easier to put into particles than to take out again. See chapter 11.)
In fact, the Koulomb force would also produce repulsion between equal
sarges, if its field energy was negative instead of positive. Just
change the sign of the constant ![]()
As the previous subsection noted, you might assume that the
electrodynamic Lagrangian, and hence the Hamiltonian, would have the
opposite sign. But that does not help. In that case the vector
potentials ![]()
To be sure, it is not completely sure that the universe will be blown to smithereens. A negative field energy only says that it is in theory possible to extract limitless amounts of energy out of the field. But you would still need some actual mechanism to do so. There might not be one. Nature might be carefully constrained so that there is no dynamic mechanism to extract the energy.
In that case, there might then be some mathematical expression for the constraint. As another way to look at that, suppose that you would indeed have a highly unstable system. And suppose that there is still something recognizable left at the end of the first day. Then surely you would expect that whatever is left is special in some way. That it obeys some special mathematical condition.
So presumably, the electromagnetic field that we observe obeys some
special condition, some constraint. What could this constraint be?
Since this is very basic physics, you would guess it to be relatively
simple. Certainly it must be Lorentz invariant. The simplest
condition that meets this requirement is that the dot product of the
four-gradient ![]()
![]()
Please note that the Lorenz condition is named after the Danish physicist Ludvig Lorenz, not the Dutch physicist Hendrik Lorentz. Almost all my sources mislabel it the Lorentz condition. The savior of the universe deserves more respect. Always remember: the Lorenz condition is Lorentz invariant.
(You might wonder why the first term in the Lorenz condition does not
have the minus sign of dot products. One way of thinking about it is
that the four-gradient in its natural
condition
already has a minus sign on the time derivative. Physicists call it a
covariant
four-vector rather than a
contravariant
one. A better way to see it is to grind
it out; you can use the Lorentz transform (1.6) of chapter
1.2.1 to show directly that the above form is the same
for different observers. But those familiar with index notation will
recognize immediately that the Lorenz condition is Lorentz invariant
from the fact that it equals ![]()
![]()
![]()
To be sure, the Lorenz condition can only be true if the interaction
with matter does not produce violations. To check that, the evolution
equation for the Lorenz condition quantity can be obtained from the
Klein-Gordon equations of the previous subsection. In particular, in
vector notation take ![]()
![]()
![]()
![]()
This important result is known as “Maxwell’s continuity equation.” It expresses conservation of charge. (To see that, take any arbitrary volume. Integrate both sides of the continuity equation over that volume. The left hand side then becomes the time derivative of the charge inside the volume. The right hand side becomes, using the [divergence] [Gauss] [Ostrogradsky] theorem, the net inflow of charge. And if the charge inside can only change due to inflow or outflow, then no charge can be created out of nothing or destroyed.) So charge conservation can be seen as a consequence of the need to maintain the Lorenz condition.
Note that the Lorenz condition (A.138) looks mathematically just like the continuity equation. It produces conservation of the integrated electrostatic potential. In subsection A.22.7 it will be verified that it is indeed enough to produce a stable electromagnetic field. One with meaningfully defined energies that do not run off to minus infinity.
Note that charge conservation by itself is not quite enough to ensure that the Lorenz condition is satisfied. However, if in addition the Lorenz quantity and its time derivative are zero at just a single time, it is OK. Then (A.139) ensures that the Lorenz condition remains true for all time.
The ideas of the previous subsection provide one way to quantize the electromagnetic field, [[17, 6]].
As already seen in subsection A.22.3 (A.128), in
quantum field theory the potentials become quantum fields,
i.e. operator fields. For electromagnetics the quantum field
four-vector is a bit more messy
![\begin{displaymath}
\widehat{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspac...
...k}\cdot{\skew0\vec r}}\widehat a^\dagger _{{\vec k}\nu}\right)
\end{displaymath}](img4612.gif)
polarizationsof the electromagnetic field. That is why they are typically aligned with the momentum of the wave rather than with some Cartesian axis system and its time axis. Note that each polarization vector has its own annihilation operator
(Electromagnetic waves in empty space are special; for them only two independent polarizations are possible. Or to be precise, even in empty space the Klein-Gordon equations with Lorenz condition allow a third polarization. But these waves produce no electric and magnetic fields and contain no net electromagnetic energy. So they are physically irrelevant. You can call them “gage equivalent to the vacuum.” That sounds better than irrelevant.)
The Lorenz condition of the previous subsection is again needed to get rid of negative energy states. The question is now exactly how to phrase the Lorenz condition in quantum terms.
(There is an epidemic among my, highly authorative, sources that come up with negative norm states without Lorenz condition. Now the present author himself is far from an expert on quantum field theories. But he knows one thing: norms cannot be negative. If you come up with negative norms, it tells you nothing about the physics. It tells you that you are doing the mahematics wrong. I believe the correct argument goes something like this: “Suppose that we can do our usual stupid canonical quantization tricks for this system. Blah Blah. That gives negative norm states. Norms cannot be negative. Ergo: we cannot do our usual stupid canonical quantization tricks for this system.” If you properly define the creation and annihilation operators to put photons in negative energy states, there is no mathematical problem. The commutator relation for the negative energy states picks up a minus sign and the norms are positive as they should. Now the mathematics is sound and you can start worrying about problems in the physics. Like that there are negative energy states. And maybe lack of Lorentz invariance, although the original system is Lorentz invariant, and I do not see what would not be Lorentz invariant about putting particles in the negative energy states.)
The simplest idea would be to require that the quantum field above
satisfies the Lorenz condition. But the quantum field determines the
dynamics. Like in the classical case, you do not want to change the
dynamics. Instead you want to throw certain solutions away. That
means that you want to throw certain wave functions ![]()
The strict condition would be to require (in the Heisenberg picture
{A.12})
But the above strict condition is too restrictive. Not even the vacuum
state with no photons would be physically observable. That is because
the creation operators in ![]()
![]()
You might of course wonder why the annihilation terms are indicated by
a plus sign, instead of the creation terms. After all, it are the
creation operators that create more photons. But the plus sign
actually stands for the fact that the annihilation terms are
associated with an ![]()
![]() .
.![]()
![]()
normal
is represented by a plus sign. Is not
addition more normal than subtraction? Please do not pull at your
hair like that, there are less drastic ways to save on professional
hair care.
Simply dropping the creation terms may seem completely arbitrary. But
it actually has some physical logic to it. Consider the inner product
There are other ways to do quantization of the electromagnetic field. The quantization following Fermi, as discussed in subsection A.22.8, can be converted into a modern quantum field theory. But that turns out to be a very messy process indeed, [[17, 6]]. The derivation is essentially to mess around at length until you more or less prove that you can use the Lorenz condition result instead. You might as well start there.
It does turns out that the so-called path-integral
formulation of quantum mechanics does a very nice job here,
[53, pp. 30ff]. It avoids many of the contortions of
canonical quantization like the ones above.
In fact, a popular quantum field textbook, [35, p. 79], refuses to do canonical quantization of the electromagnetic field at all, calling it an awkward subject. This book is typically used during the second year of graduate study in physics, so it is not that its readers are unsophisticated.
Returning to the classical electromagnetic field, it still needs to be examined whether the Lorenz condition has made the universe safe for life as we know it.
The answer depends on the Lagrangian, because the Lagrangian
determines the evolution of a system. So far, the Lagrangian has been
written in terms of the four potentials ![]()
![]()
![]()
![]()
![]() .
.
With a bit of mathematical manipulation, {D.37.3}, the
self-evident electromagnetic Lagrangian density can be written as:
The term inside the curly brackets is zero according to the Lorenz condition (A.138). Therefore, it too does not affect the motion. (To be precise, the term does not affect the motion because it is squared. By itself it would affect the motion. In the formal way in which the Lagrangian is differentiated, one power is lost.)
The conventional Lagrangian density is found by disregarding the terms
that do not change the motion:
As an aside, it might be noted that physicists find the above
expression too intuitive. So you will find it in quantum field books
in relativistic index notation as:
Because the conventional Lagrangian density is different from the self-evident one, the field equations (A.135) and (A.136) for the potentials pick up a few additional terms. To find them, repeat the analysis of subsection A.22.4 but use the conventional density above in (A.134). Note that you will need to write the electric and magnetic fields in terms of the potentials using (A.131). (Using the field strength tensor is actually somewhat simpler in converting to the potentials. If you can get all the blasted sign changes right, that is.)
Then the conventional field equations become:
The additional terms in each equation above are the two before the equals signs. Note that these additional terms are zero on account of the Lorenz condition. So they do not change the solution.
The conventional field equations above are obviously more messy than the original ones. Even if you cancel the second order time derivatives in (A.140). However, they do have one advantage. If you use these conventional equations, you do not have to worry about satisfying the Lorenz condition. Any solution to the equations will give you the right electric and magnetic fields and so the right motion of the charged particles.
To be sure, the potentials will be different if you do not satisfy the Lorenz condition. But the potentials have no meaning of their own. At least not in classical electromagnetics.
To verify that the Lorenz condition is no longer needed, first recall
the indeterminacy in the potentials. As subsection A.22.4
discussed, more than one set of potentials can produce the same
electric and magnetic fields. In particular, given potentials
![]()
![]() ,
,
gage transform.
Now suppose that you have a solution ![]()
![]()
![]()
![]()
Now it turns out that the new potentials ![]()
![]()
![]()
![]()
The evolution equation (A.140) for the electrostatic field is
worth a second look. Because of the definition of the electric field
(A.130), it can be written as
Maxwell’s first equation,chapter 13.2. It ties the charge density to the electric field quite rigidly.
Maxwell’s first equation is a consequence of the Lorenz condition. It would not be required for the original Klein-Gordon equations without Lorenz condition. In particular, it is the Lorenz condition that allows the additional two terms in the evolution equation (A.140) for the electrostatic potential. These then eliminate the second order time derivative from the equation. That then turns the equation from a normal evolution equation into a restrictive spatial condition on the electric field.
It may be noted that the other evolution equation (A.141) is Maxwell’s fourth equation. Just rewrite it in terms of the electric and magnetic fields. The other two Maxwell equations follow trivially from the definitions (A.130) of the electric and magnetic fields in terms of the potentials.
Since there is no Lorenz condition for the conventional equations, it becomes interesting to find the corresponding Hamiltonian. That should allow the stability of electromagnetics to be examined more easily.
The Hamiltonian for electromagnetic field plus a proton may be found
the same way as (A.137) in subsection A.22.5,
{A.1.5}. Just use the conventional Lagrangian
density instead. That gives
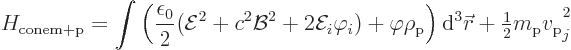
The simplified energy above is no longer really a Hamiltonian; you cannot write Hamilton’s equations based on it as in {A.1.5}. But it does still give the energy that is conserved.
The energy above is always positive. So it can no longer be lowered by arbitrary amounts. The system will not blow up. And that then means that the original Klein-Gordon equations (A.135) and (A.136) for the fields are stable too as long as the Lorenz condition is satisfied. They produce the same evolution. And they satisfy the speed of light restriction and are Lorentz invariant. Lorenz did it!
Note also the remarkable result that the interaction energy between proton charge and field has disappeared. The proton can no longer minimize any energy of interaction between itself and the field it creates. Maxwell’s first equation is too restrictive. All the proton can try to do is minimize the energy in the electric and magnetic fields.
Quantizing the electromagnetic field is not easy. The previous
subsection showed a couple of problems. The gage property implies
that the electromagnetic potentials ![]()
![]()
![]() .
.
Various ways to deal with that have been developed. The quantization procedure discussed in this subsection is a simplified version of the one found in Bethe’s book, [6, pp. 255-271]. It is due to Fermi, based on earlier work by Dirac and Heisenberg & Pauli. This derivation was a great achievement at the time, and fundamental to more advanced quantum field approaches, [6, p. 266]. Note that all five mentioned physicists received a Nobel Prize in physics at one time or the other.
The starting point in this discussion will be the original potentials
![]()
![]()
It was Fermi who recognized that you can make things a lot simpler for
yourself if you write the potentials as sums of exponentials of the
form ![]() :
:
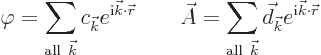
Fourier modes.The principle is the same. The constant vector
Note that the coefficients ![]()
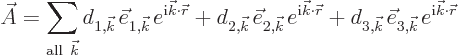
longitudinal.The other two unit vectors should be orthogonal to the first component and to each other. That still leaves a bit choice in direction. Fortunately, in practice it does not really make a difference exactly how you take them. The corresponding electromagnetic waves are called
transverse.
In short, the fields can be written as
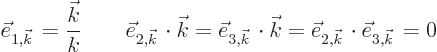
From those expressions, and the directions of the unit vectors, it can
be checked by straight substitution that the curl
of
the longitudinal potential is zero:
The same way, it turns out that that the divergence
of
the transverse potential is zero
To be fair, Fermi did not really discover that it can be smart to take vector fields apart into irrotational and solenoidal parts. That is an old trick known as the “Helmholtz decomposition.”
Since the transverse potential has no divergence, the longitudinal potential is solely responsible for the Lorenz condition (A.138). The transverse potential can do whatever it wants.
The real problem is therefore with the longitudinal potential
![]()
![]() .
.
Reconsider the expressions (A.130) for the electric and magnetic fields in terms of the potentials. They show that the electrostatic potential produces no magnetic field. And neither does the longitudinal potential because it is irrotational.
They do produce a combined electric field
![]() .
.![]()
![]()
Coulomb potential.
As far as the divergence of the electric field
![]()
Now suppose that you replaced the electrostatic field ![]()
![]()
![]()
So why not? To be sure, the combination of the Coulomb potential
![]()
![]()
Instead of the Lorenz condition, the combination of Coulomb potential
plus transverse potential satisfies the so-called “Coulomb condition:”
| (A.145) |
Lorenz gage,while the new ones use the
Coulomb gage.
Because the potentials ![]()
![]()
Now consider the Coulomb potential somewhat closer. As noted above
it satisfies the Poisson equation
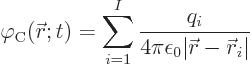 |
(A.146) |
If the charge distribution ![]()
point charges
![]() .
.
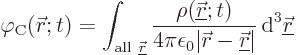 |
(A.147) |
The key point to note here is that the Coulomb potential has no life of its own. It is rigidly tied to the positions of the charges. That then provides the most detailed answer to the question: “What happened to energy minimization?” Charged particles have no option of minimizing any energy of interaction with the field. Maxwell’s first equation, the Poisson equation above, forces them to create a Coulomb field that is repulsive to them. Whether they like it or not.
Note further that all the mechanics associated with the Coulomb field is quasi-steady. The Poisson equation does not depend on how fast the charged particles evolve. The Coulomb electric field is minus the spatial gradient of the potential, so that does not depend on the speed of evolution either. And the Coulomb force on the charged particles is merely the electric field times the charge.
It is still not obvious how to quantize the Coulomb potential, even
though there is no longer a longitudinal field. But who cares about
the Coulomb potential in the first place? The important thing is how
the charged particles are affected by it. And the forces on the
particles caused by the Coulomb potential can be computed using the
electrostatic potential energy, {D.37.4},
Incidentally, note the required omission of the terms with ![]()
![]()
![]()
The issue does not exist if the charge is smoothly distributed. In
that case the Coulomb potential energy is, {D.37.4},
So the big idea is to throw away the electrostatic and longitudinal
potentials and replace them with the Coulomb energy
![]() ,
,
First, consider the Fermi Lagrangian. It is found by throwing out the
electrostatic and longitudinal potentials from the earlier Lagrangian
(A.134) and subtracting ![]() .
.
![\begin{displaymath}
{\cal L}_{\rm F} = \frac{\epsilon_0}{2}
\int \bigg[\left\v...
...+ {\textstyle\frac{1}{2}} m_i \vec v_i^{\,2} \Big] - V_{\rm C}
\end{displaymath}](img4662.gif) |
(A.150) |
You may wonder how you can achieve that only the transverse potential
![]()
The unknowns are now no longer the values of the potential at the
infinitely many possible positions. Instead the unknowns are now the
coefficients ![]()
![]()
(The ![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
The Hamiltonian can be obtained just like the earlier one
(A.137), {A.1.5}. (Or make that
{A.1.4}, since the unknowns, ![]()
![]() ,
,![]() .
.![]()
![\begin{displaymath}
{\cal L}_{\rm F} = \frac{\epsilon_0}{2}
\int \sum_{j=1}^3 ...
... + {\textstyle\frac{1}{2}} m_i v_i\strut_j^2 \Big] - V_{\rm C}
\end{displaymath}](img4668.gif)
Now Hamiltonians should not be in terms of particle velocities,
despite what (A.137) said. Hamiltonians should be in terms
of canonical momenta,
{A.1.4}. The
canonical momentum corresponding to the velocity component
![]()
![]()
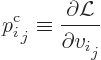
The time derivatives of the real and imaginary parts of the
coefficients ![]()
![]()
The Hamiltonian then becomes, following {A.1.4} and
in vector notation,
In terms of the waves (A.144), the integral falls apart in
separate contributions from each ![]()
![]()
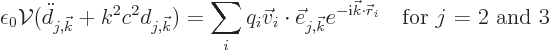
If the speed of the particle gets comparable to the speed of light,
you may want to use the relativistic energy (1.2);
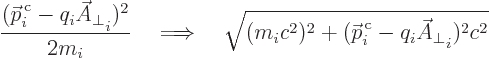
Sometimes, it is convenient to assume that the system under
consideration also experiences an external electromagnetic field. For
example, you might consider an atom or atomic nucleus in the magnetic
field produced by an electromagnet. You probably do not want to
include every electron in the wires of the electromagnet in your
model. That would be something else. Instead you can simply add the
vector potential ![]()
![]()
![]()
![]() .
.
Note that the entire external vector potential is needed, not just the
transverse part. The longitudinal part is not included in
![]() .
.
Particle spin, if any, is not included in the above Hamiltonian. At nonrelativistic speeds, its energy can be described as a dot produce with the local magnetic field, chapter 13.4.
So far all this was classical electrodynamics. But the interaction between the charges and the transverse waves can readily be quantized using essentially the same procedure as used for the Koulomb potential in subsection A.22.3. The details are worked out in addendum {A.23} for the fields. It allows a relativistic description of the emission of electromagnetic radiation by atoms and nuclei, {A.24} and {A.25}.
While the transverse field must be quantized, the Coulomb potential can be taken unchanged into quantum mechanics. That was done, for example, for the nonrelativistic hydrogen atom in chapter 4.3 and for the relativistic one in addendum {D.81}.
Finally, any external fields are assumed to be given; they are not quantized either.
Note that the Fermi quantization is not fully relativistic. In a
fully relativistic theory, the particles too should be described by
quantum fields. The Fermi quantization does not do that. So even the
relativistic hydrogen atom is not quite exact, even though it is
orders of magnitude more accurate than the already very accurate
nonrelativistic one. The energy levels are still wrong by the
so-called Lamb shift,
{A.39} But this is an
extremely tiny effect. Little in life is perfect, isn’t it?
The Coulomb potential
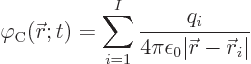
To understand what is going on, assume that at time zero some charges
at the origin are given a well-deserved kick. As mentioned earlier,
the Klein-Gordon equations respect the speed of light. Therefore the
original potentials ![]()
![]() ,
,![]()
The Coulomb potential above, however, includes the longitudinal part
![]()
![]() .
.![]()
![]()
![]()
The bottom line is
The mathematics of the Helmholtz decomposition ofThe limitation is still there, it is just much more difficult to see. The change in current densityinto and hides, but of course does not change, the limitation imposed by the speed of light.